При работе с одномерными массивами существует большое количество алгоритмов, которые считаются типовыми, т.е. часто встречающимися в практических задачах.
Перечислим основные типовые алгоритмы, используемые для работы с одномерными массивами: ввод-вывод массива, вычисление значений элементов массива, поиск суммы и (или) произведения элементов массива, поиск максимального (минимального) элемента массива, упорядочивание элементов массива, добавление (вставка) новых элементов в массив, удаление данных из массива с его сжатием и т.д.
Часть типовых алгоритмов (наиболее элементарных) мы уже рассмотрели в предыдущей теме. Здесь разберём более сложные алгоритмы, которые также считаются типовыми.
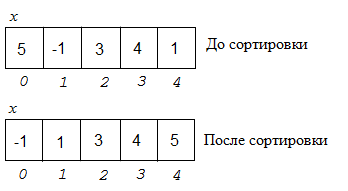
Сортировка — это перестановка элементов массива с целью расположения этих элементов в определённом порядке, например: по возрастанию или по убыванию.
Для чего упорядочивают массивы? Как правило, сортировка не является самоцелью. В упорядоченном массиве, прежде всего, быстрее (и часто проще) искать необходимую информацию.
Существует большое количество алгоритмов по упорядочиванию элементов массива, например, «пузырьковая» сортировка, метод Шелла, пирамидальная сортировка, быстрая сортировка Хоара и т.д. Для упорядочивания небольших массивов подойдёт любой метод (та же «пузырьковая» сортировка), если же массивы огромны, то требуется более эффективные методы. Одним из лучших по скорости работы считается метод быстрой сортировки Хоара.
Здесь разберём один из наиболее простых методов («пузырьковая» сортировка), а в теме «Рекурсия» можно посмотреть метод быстрой сортировки Хоара.
«Пузырьковая» сортировка
Пример. Дан массив из n целых чисел. Упорядочить этот массив по возрастанию.

Идея метода. В цикле просматриваем весь массив и сопоставляем попарно xi и xi+1 элементы. Если xi>xi+1, то делаем перестановку. Когда массив пройден до конца, то нужно решить, что делать дальше. Если при просмотре массива были перестановки, то процесс повторяем вновь, если перестановок не было, значит массив упорядочен и сортировку нужно прекратить.
Реализация алгоритма:
#include <iostream>
using namespace std;
#include <cmath>
int main()
{
int x[]={5, -1, 3, 4, 1};
int n = sizeof(x) / sizeof(int);
int c, i;
cout << "Dano " << n << " numbers:" << endl;
for(i = 0; i < n; i++)
cout << x[i] << endl;
int k = n; // Последний необработанный элемент
// Признак p=true – были перестановки, значит повторяем
// Признак p=false – перестановок нет, выход
bool p;
do{
p = false;
k--;
for(i = 0; i < k; i++)
if(x[i] > x[i+1])
{
c = x[i];
x[i] = x[i+1];
x[i+1] = c;
p = true;
}
}while(p);
// Распечатка массива
cout << "Massiv:" << endl;
for(i = 0; i < n; i++)
cout << x[i] << endl;
return 0;
}
Замечания. После каждого просмотра всего массива при использовании «пузырьковой» сортировки мы гарантированно переставляем один (последний) элемент на своё место. Поэтому после каждого просмотра есть смысл укорачивать список необработанных элементов. Здесь это делается за счёт уменьшения переменной k.
Достаточно часто из массива необходимо удалить ненужные элементы. Что означает слово удалить? Иногда бывает приемлемо «заменить», но чаще всего под этим подразумевают именно удаление, т.е. на место удалённого элемента должен быть записан тот элемент массива, который должен остаться. Элементы массива необходимо сдвинуть к какому-нибудь краю массива. Обычно сдвиг делается в сторону начала массива, чтобы индексация снова была с нуля. Рассмотрим процедуру удаления на конкретном примере.
Пример. Дан массив из n целых чисел. Удалить из него все числа, меньше нуля. Массив сжать. На рисунке ниже приведён массив x из 5 чисел до и после удаления отрицательных чисел.

Каким
образом можно решить эту задачу?
Вариант 1. Идея напрашивается сама собой. Просматриваем массив слева на право, как только находим подходящий для удаления элемент, так сразу же сдвигаем все элементы правее его на одну позицию влево.
Возможная реализация алгоритма:
#include <iostream>
using namespace std;
int main()
{
int n = 5;
int x[n];
int i, j, k;
cout << "Input " << n << " numbers:" << endl;
for(i = 0; i < n; i++)
cin >> x[i];
k = n; // Первоначально в массиве все элементы.
// Затем k будет означать количество оставшихся после удаления.
for(i = 0; i < k; i++)
{
if(x[i] < 0) // условие на удаление элемента массива
{
k--; // уменьшаем количество
for(j = i; j < k; j++) // сдвиг влево
x[j] = x[j+1];
i--; // Снова просматриваем i-й элемент
}
}
cout << "Otvet:" << endl;
for(i = 0; i < k; i++)
cout << x[i] << endl;
return 0;
}
Маленькое замечание. Если подходящий для удаления элемент найден, то после сдвига необходимо снова проверять элемент в этой же позиции, так как следом за только-что удалённым элементом может идти элемент массива, который также является кандидатом на удаление. В программе цикл for обеспечивает переход к следующему элементу, а оператор i--; позволяет снова при последующей итерации проверять тот же i-1 элемент.
Вариант 2. Если внимательно посмотреть только-что рассмотренный алгоритм, то несложно понять, что в нём есть лишняя «работа»: мы сдвигаем влево некоторые элементы, которые в последствии удалим. Можно ли избавиться от этого? Можно, если вести проверку с конца массива. Тогда сдвигать влево будем только остающиеся в массиве элементы.
Возможная реализация алгоритма:
#include <iostream>
using namespace std;
int main()
{
int n = 5;
int x[n];
int i, j, k;
cout << "Input " << n << " numbers:" << endl;
for(i = 0; i < n; i++)
cin >> x[i];
k = n; // Первоначально в массиве все элементы.
// Затем k будет означать количество оставшихся после удаления.
for(i = k-1; i >= 0; i--)
{
if(x[i] < 0) // условие на удаление элемента массива
{
k--; // уменьшаем количество
for(j = i; j < k; j++) // сдвиг
x[j] = x[j+1];
}
}
cout << "Otvet:" << endl;
for(i = 0; i < k; i++)
cout << x[i] << endl;
return 0;
}
Вариант 3. Если удаляемых элементов много, то оба приведённые алгоритмы работают довольно медленно. Для повышения скорости работы надо сразу переставлять оставшийся элемент на своё место, а не сдвигать каждый раз на одну позицию.
Возможная реализация алгоритма:
#include <iostream>
using namespace std;
int main()
{
int n = 5;
int x[n];
int i, j, k;
cout << "Input " << n << " numbers:" << endl;
for(i = 0; i < n; i++)
cin >> x[i];
k = 0; // Вначале это позиция, в которую отправляем оставшийся элемент.
// Затем k будет означать количество оставшихся после удаления элементов.
for(i = 0; i < n; i++)
{
if(!(x[i] < 0)) // условие не на удаление элемента из массива,
// а на оставление (!!) его в массиве
{
x[k] = x[i];
k++;
}
}
cout << "Otvet:" << endl;
for(i = 0; i < k; i++)
cout << x[i] << endl;
return 0;
}
Замечания. 1)Как видим, здесь при удалении используется одинарный цикл, а не двойной, как в первых вариантах. Скорость работы всегда выше. 2)Надо записывать условие не на удаление, а на оставление элемента в массиве. В нашем примере лучше было бы записать if(x[i] >= 0). Условие с отрицанием if(!(x[i] < 0)) дано только для пояснения идеи.
Вариант 4. Любопытная мысль — использовать метод «пузырьковой сортировки» для удаления данных из массива, — была предложена студенткой 1-го курса Абрамовой Антониной (группа 2102, март 2008г). Скорость работы этого варианта, конечно, невысокая. Она даже ниже, чем у первого варианта. Но мысль интересная!
Реализация алгоритма:
#include <iostream>
using namespace std;
int main()
{
const int n=5;
int x[n];
int i, k, c;
bool pr;
cout << "Input " << n << " numbers:" << endl;
for(i=0; i < n; i++)
cin >> x[i];
// Вначале перемещаем удаляемые данные в конец массива
k=n-1;
do{
pr = false;
for(i=0; i<k; i++)
if(x[i] < 0 && x[i+1] >= 0) // Условие для обмена:
// слева - удаляемый элемент, справа - тот, что надо оставить в массиве
{
c = x[i];
x[i] = x[i+1];
x[i+1] = c;
pr = true;
}
k--;
}while(pr);
// Подсчет количества оставшихся после удаления элементов массива
for(i = n-1, k = n; i >=0; i--)
if(x[i] < 0) // это удаленный элемент - значит
k--; // уменьшаем количество элементов массива
cout << "Result massiv:" << endl;
for(i=0; i < k; i++)
cout << x[i] << endl;
return 0;
}
Вариант 5. А вот ещё один очень хороший вариант решения той же задачи (удаление всех отрицательных чисел из массива), который предложила студентка 1 курса Ерусланова Надежда (группа 2102, март 2011г). Скорость работы этого метода гораздо выше, чем у методов 1, 2 и 4, но немного ниже, чем у 3-го. Привожу авторский текст программы без изменений:
#include <iostream>
using namespace std;
int main()
{
const int n=10;
double x[n];
int i,j,k,f=0;
for(i=0;i<n;i++)
{
cout << "x["<<i<<"]="; cin>>x[i];
if (x[i]>=0) f++; } //я не смогла придумать нормальный счетчик, поэтому так=)
for(i=0; i<n; i++)
if(x[i]<0)
{
k=i;
for(j=i+1; j<n; j++)
if(x[j]>=0)
{
x[k]=x[j];
x[j]=-1;
break;
}
}
for (i=0;i<f;i++)
cout<<x[i]<<" ";
cout<<endl;
return 0;
}
Замечания по всем пяти вариантам.
1)Если массив небольшой, то для удаления можно использовать любой вариант. Для больших массивов наилучшим будет, конечно же, 3-й вариант. И чем больше данных удаляется из массива, тем этот вариант выгоднее.
2)В ряде задач требуется удалить не все элементы, отвечающие какому-то условию, а заданное количество, например, первые 3 отрицательных или 2 последних ненулевых.
2а)Для удаления первых T элементов, отвечающих данному условию, подойдёт 1-й вариант (достаточно в цикле добавить дополнительную проверку), например, так:
for(t = 0, i = 0; i < k && t < T; i++)
{
if(x[i] < 0) // условие на удаление элемента массива
{
t++; // количество удалённых на данный момент элементов
k--; // уменьшаем количество
for(j = i; j < k; j++) // сдвиг влево
x[j] = x[j+1];
i--; // Снова просматриваем i-й элемент
}
}
2б)Для удаления последних R элементов, отвечающих данному условию, подойдёт 2-й вариант (также надо подсчитывать количество уже удалённых элементов, сделать это можно по аналогии с рассмотренным только что вариантом 2а).
Не менее часто применяется на практике и вставка данных в массив. Что можно здесь увидеть интересного?
Прежде всего надо понимать, что при добавлении данных в массив их количество будет возрастать. А это значит, что надо заранее позаботится о выделении нужного количества памяти под массив.
Например, если ставится задача «перед каждым числом», отвечающим какому-то условию, «добавить новый элемент», то сколько необходимо выделять памяти? В массиве может не оказаться ни одного элемента, отвечающего заданному условию, а могут и все элементы подходить под данное условие. Значит, надо учитывать худший вариант. В данном случае необходимо выделить памяти под 2·n элементов массива.
Второе. Данные можно добавлять перед элементом, отвечающим заданному условию, а можно — после такого элемента. Это определяется условием решаемой задачи.
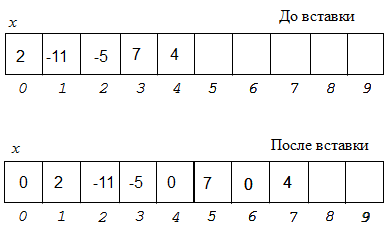
Пример. Дан массив из n целых чисел. Перед каждым положительным числом добавить число 0.
Возможная реализация алгоритма:
#include <iostream>
using namespace std;
int main()
{
int n = 5;
int x[2*n];
int i, j, k;
cout << "Input " << n << " numbers:" << endl;
for(i = 0; i < n; i++)
cin >> x[i];
k = n; // Первоначально в массиве все элементы.
// Затем k будет означать количество после добавления.
for(i = 0; i < k; i++)
{
if(x[i] > 0) // условие на вставку элемента массива
{
for(j = k; j > i; j--) // сдвиг в право
x[j] = x[j-1];
x[i] = 0; // вставка нового элемента
k++; // увеличиваем количество
i++; // делаем обход уже обработанного элемента
}
}
cout << "Otvet:" << endl;
for(i = 0; i < k; i++)
cout << x[i] << endl;
return 0;
}
Алгоритм вставки после элемента, отвечающего требованиям задачи, не сложнее только-что рассмотренного. Попробуйте его реализовать самостоятельно.
|
|
|
|