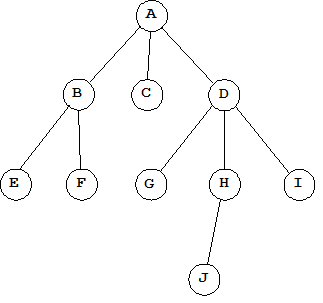
Дерево — это нелинейная динамическая структура данных, представленных в виде иерархии элементов, называемых узлами. Схематично дерево можно изобразить так, как показано на рисунке ниже:

На самом верхнем уровне такой иерархии всегда имеется только один узел, называемый корнем дерева. У нас это узел A. Каждый узел, кроме корневого, связан только с одним узлом более высокого уровня, называемым узлом-предком. Например, для узла D предком является узел A, предок для узла G — это D и т.д. При этом каждый элемент дерева может быть связан с помощью ветвей (ребер) с одним или несколькими узлами более низкого уровня. Они для данного узла являются дочерними узлами (узлами-потомками). Так, для узла A потомками будут B, C и D, для узла B — E и F и т.д. Элементы, расположенные в конце ветвей и не имеющие дочерних узлов, называют листьями. На рисунке выше листьями являются узлы E, F, C, G, J и I.
От корня до любого узла всегда существует только один путь. Максимальная длина пути от корня до листьев называется высотой дерева. У нас максимально длинный путь образует цепочка узлов A, D, H и J, т.е. высота дерева равна 3.
Любой узел дерева с его потомками также образует дерево, называемое поддеревом (относительно исходного дерева). Например, можно рассматривать поддерево, начинающееся с узла D (это узлы D, G, H, I, J).
Число поддеревьев для данного узла образует степень узла. Для узлов A и D степень равна 3, степень узла B равна 2, узел H имеет степень 1, а у листьев (узлы E, F, C, G, J и I) степень равна 0. Максимальное значение среди степеней всех узлов определяет степень дерева. Если максимальная степень узлов в каком-то дереве равна n, то его называют n-арным деревом. Наше дерево имеет степень 3 (из-за узлов A и D), и его можно называть триарным.
Дерево степени 2 называется бинарным. Бинарные деревья наиболее просты с точки зрения сложности реализации алгоритмов работы с деревьями, поэтому именно бинарные деревья применяются там, где требуется динамическая структура типа дерево. Если формально требуется дерево степени большей, чем 2, например, 5-й степени, то, сформировав такое дерево, его можно преобразовать в бинарное, а далее работать как с бинарным деревом.
Как правило, в дереве всегда задают какой-либо принцип упорядоченности, например, по возрастанию какого-то параметра (ключа). То есть, для каждого узла ключи наследников располагаются слева направо по возрастанию. В бинарном дереве для каждого узла значение ключа левого наследника будет меньше значения ключа узла, в свою очередь значение ключа в узле меньше значения ключа в правом наследнике.
Для работы с двоичными деревьями используем две структуры:
1)Структура, содержащая собственно сами данные. Она может иметь любое количество полей. Одно из полей (или совокупность из нескольких полей) будет ключевым. Именно по нему будет вестись упорядочивание данных. Для рассматриваемой ниже задачи нам достаточно одного поля, которое будет ключом:
struct Data
{
int a;
};
2)Структура, определяющая узел дерева:
struct Tree
{
Data d;
Tree *left;
Tree *right;
};
Здесь используем два указателя:
left — указатель на левого наследника;
right — указатель на правого наследника.
Тексты этих структур необходимо расположить в начале программы (до main() и других функций).
В программе (обычно в функции main()) определяем указатель на корень дерева:
Tree *u = 0;
Первоначально дерево пусто, и указатель равен 0.
Теперь у нас всё готово для того, чтобы приступить к работе с бинарным деревом. Все действия для наглядности рассмотрим на конкретном примере.
Пример. Пусть дана числовая последовательность: 10, 25, 20, 6, 21, 8, 1, 30. Необходимо построить двоичное дерево. Данные упорядочивать по возрастанию.
Решение. Первым числом в последовательности является число 10. Именно оно заносится в корневой узел. Затем идет число 25. Оно меньше ключевого поля в корне, следовательно 25 добавляем к правой ветви корня. Число 20 больше 10, но меньше 25, поэтому оно добавится к левой ветви для узла, содержащего число 25. И так далее. В итоге получим дерево, изображённое на рисунке ниже:

Рассмотрим основные операции по работе с двоичным деревом. Везде u — это указатель на корень дерева.
1. Добавление нового элемента:
void Add(Tree **u, Data &x)
{
Tree *p = *u;
if(p == 0)
{ // Дерево пусто - добавляемый новый элемент станет корнем дерева
p = new Tree;
p->d.a = x.a;
p->left = 0;
p->right = 0;
*u = p;
return;
}
Tree *p1;
bool priznak = false; // признак того, что такой элемент уже имеется
while(p && !priznak)
{
p1 = p;
if(x.a == p->d.a)
priznak = true;
else
if(x.a < p->d.a)
p = p->left;
else
p = p->right;
}
if(priznak) return;
// Создание нового узла
Tree *pnew = new Tree;
pnew->d.a = x.a;
pnew->left = 0;
pnew->right = 0;
if(x.a < p1->d.a) // присоединить к левому поддереву
p1->left = pnew;
else // присоединить к правому поддереву
p1->right = pnew;
}
Возможный вызов функции:
Add(&u, x);
где x — объект типа Data.
Замечание. Многократный вызов в цикле этой функции с новыми x позволяет сформировать первоначальное дерево (как в нашем примере).
2. Обход дерева и вывод значений узлов в упорядоченном виде (по возрастанию) на экран монитора:
void Print(Tree *u)
{
if(u)
{
Print(u->left);
cout << u->d.a << endl;
Print(u->right);
}
}
Возможный вызов функции:
Print(u);
3. Поиск узла, ключ которого равен заданному значению:
Tree* Find(Tree *u, Data &x, Tree **prev)
{
Tree *p = u;
*prev = 0;
// Дерево пусто - искать нечего
if(p == 0)
return 0;
// Поиск искомого элемента
while(p)
{
//cout << "Find : " << p->d.a << endl;
if(p->d.a == x.a) // Решение найдено
return p;
if(p->d.a > x.a) // Перейти на левое поддерево
{
*prev = p;
p = p->left;
}
else// Перейти на правое поддерево
{
*prev = p;
p = p->right;
}
}
// Если попадаем сюда - значит решение не существует
*prev = 0;
return 0;
}
Возможный вызов функции:
Tree *p = Find(u, x, &p0);
Данная функция возвращает адрес найденного узла (если узел не найден, то результат равен 0).
Дополнительно через список параметров возвращается адрес узла-предка p0 для искомого узла. Если решение не найдено или искомый узел — это корень, то p0=0. А x, как обычно — объект типа Data.
4. Удаление элемента из дерева:
void Delete(Tree **u, Data &x)
{
Tree *p0 = 0;
Tree *p = Find(*u, x, &p0);
// Ничего не найдено - удалять не чего
if(p == 0)
return;
// Найденный элемент - корень дерева и надо удалять этот корень
if(p0 == 0 && (p->left == 0 || p->right == 0))
{
if(p->left == 0 && p->right == 0)
*u = 0;
else if(p->left == 0)
*u = p->right;
else
*u = p->left;
delete p;
return;
}
// Найденный элемент - это лист
if(p->left == 0 && p->right == 0)
{
if(p0)
{
if(p0->left == p)
p0->left = 0;
else
p0->right = 0;
}
else// лист оказался корнем!
u = 0;
delete p;
return;
}
// Найденный элемент - промежуточный узел по левой ветви, вырожденной в список
if(p->left != 0 && p->right == 0)
{
if(p0->left == p)
p0->left = p->left;
else
p0->right = p->left;
delete p;
return;
}
// Найденный элемент - промежуточный узел по правой ветви, вырожденной в список
if(p->left == 0 && p->right != 0)
{
if(p0->left == p)
p0->left = p->right;
else
p0->right = p->right;
delete p;
return;
}
// общий случай
if(p->left != 0 && p->right != 0)
{
p0 = p;
Tree *t = p->left;
while(t->right)
{
p0 = t;
t = t->right;
}
p->d.a = t->d.a;
if(p0->left == t)
p0->left = 0;
else
p0->right = 0;
delete t;
}
}
Возможный вызов функции:
Delete(&u, x);
где x — объект типа Data.
Функция Delete() использует функцию Find() для поиска удаляемого объекта. Именно для функции Delete() в списке параметров Find() применён дополнительный параметр p0 — адрес узла, который является предком удаляемого узла.
5. Удаление (очистка) всего дерева
После завершения работы с данными, хранящимися в дереве, необходимо очистить всё дерево. Выполнять это действие желательно сразу же, как дерево стало не нужным. Реализация этой операции может быть такой:
// Очистка всего дерева
void Clear(Tree **u)
{
if(*u == 0) return;
Clear1(u);
cout << "delete (*u)->d.a=" << (*u)->d.a << endl;
delete *u;
*u=0;
}
void Clear1(Tree **u0)
{
Tree *t;
Tree *u = *u0;
if(u->left != 0)
{
if(u->left->left != 0 || u->left->right != 0)
Clear1(&(u->left));
if(u->left->left == 0 && u->left->right == 0)
{
cout << "delete u->left->d.a=" << u->left->d.a << endl;
t = u->left;
delete t;
u->left = 0;
}
}
if(u->right != 0)
{
if(u->right->left != 0 || u->right->right != 0)
Clear1(&(u->right));
if(u->right->left == 0 && u->right->right == 0)
{
cout << "delete u->right->d.a=" << u->right->d.a << endl;
t = u->right;
delete t;
u->right = 0;
}
}
}
Возможный вызов функции:
Clear(&u);
Функция Clear() содержит вызов дополнительной рекурсивной функции Clear1(), в которой делается очистка всего дерева, кроме корня. Корневой узел удаляется затем непосредственно в функции Clear().
Алгоритм функции Clear() предельно прост и не требует каких-то дополнительных пояснений. А вот о работе Clear1() есть смысл поговорить немного подробнее.
Итак, при очередном рекурсивном вызове функции Clear1() делается проверка: имеется ли у текущего узла «левый наследник» u->left ? Если «да», то проверяем, является этот «наследник» листом, или он также имеет хотя бы одного «наследника». Если u->left — это лист, то его удаляем, иначе делаем на него переход, т.е. рекурсивно вызываем Clear1() для текущего «левого наследника». Всё то же самое делается и для правого наследника u->right. Работа продолжается до тех пор, пока в дереве не останется только один корень, который будет удалён в функции Clear().
Для лучшего понимания алгоритма работы очистки всего дерева в функциях Clear() и Clear1() имеется дополнительная печать. Если дерево было заполнено числовой последовательностью: 10, 25, 20, 6, 21, 8, 1, 30, то на экране будет выведено следующее:
delete u->left->d.a=1
delete u->right->d.a=8
delete u->left->d.a=6
delete u->right->d.a=21
delete u->left->d.a=20
delete u->right->d.a=30
delete u->right->d.a=25
delete (*u)->d.a=10
Именно в такой порядке будут удаляться узлы дерева.
|
|
|
|