Через список параметров в подпрограмму можно передавать не только данные и (или) адреса областей памяти, где хранятся какие-либо данные, но и адреса других функций. Где это может пригодиться?

Предположим, необходимо написать программу для вычисления определённого интеграла , например, по методу трапеций. Идея метода проста и её легко понять из рисунка:

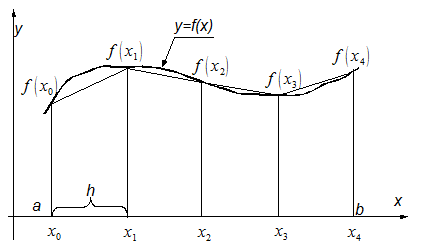
Приближённое значение интеграла S можно представить как сумму площадей элементарных трапеций. Пусть количество отрезков n=4. Тогда

=

=

В общем случае, получим такую формулу:

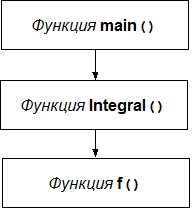
Функции по реализации метода и по вычислению подынтегральной функции логично оформить в виде отдельных подпрограмм. Схема вызова функций выглядит так:

Для конкретики вычислим при n=20. Здесь точный ответ равен 7/3.

Возможный вариант программы:

#include <iostream>

using namespace std;

double f(double x);

double Integral(double a, double b, int n);

int main()

{

   int n = 20;

   double a = 1, b = 2;

   double y = Integral(a, b, n);

   cout << "y="<< y << endl;

   return 0;

}

// Функция для вычисления определённого интеграла по методу трапеций

double Integral(double a, double b, int n)

{

   double s = (f(a) + f(b))/2, h = (b - a) / n, x = a + h;

   for(int i = 1; i < n; i++, x += h)

      s += f(x);

   s *= h;

   return s;

}

// Подынтегральная функция

double f(double x)

{

   return x*x;

}

Результат вычисления:

y=2.33375

Как видно из текста программы, реализация метода трапеций ни как не зависит от вычисления подынтегральной функции.

Проблем нет, если подынтегральная функция одна, а если надо подсчитать, к примеру, сумму интегралов, у которых разные подынтегральные функции? На рисунке ниже показано два участка интегрирования:

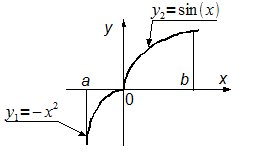
В реальных практических задачах их может быть любое количество. Напрашивается мысль передавать имя подынтегральной функции в функцию, реализующую метод интегрирования, например, в нашу Integral(), чтобы там использовать некоторое формальное имя (хотя бы f()). Естественно, все функции, которые будут передаваться через список параметров, должны иметь одинаковый список параметров и одинаковый тип результата. Отличаться они будут только в именах и, наверняка, в реализации.

Возможный вариант программы:

#include <iostream>

#include <cmath>

using namespace std;

double f1(double x);

double f2(double x);

double Integral(double (*f)(double x), double a, double b, int n);

int main()

{

   int n = 20;

   const double PI=3.14159265;

   double a = -1, b = PI/2;

   double y = Integral(f1, a, 0, n) + Integral(f2, 0, b, n);

   cout << "y=" << y << endl;

   return 0;

}

// Функция для вычисления определённого интеграла по методу трапеций

double Integral(double (*f)(double x), double a, double b, int n)

{

   double s = (f(a) + f(b))/2, h = (b - a) / n, x = a + h;

   for(int i = 1; i < n; i++, x += h)

      s += f(x);

   s *= h;

   return s;

}

// Подынтегральные функции

double f1(double x)

{

   return -x*x;

}

double f2(double x)

{

   return sin(x);

}

В этом примере при вызове функции Integral () первым параметром указывается имя нужной подынтегральной функции (у нас f1() и f2()). В прототипе функции Integral() и, естественно, в её заголовке при определении первым параметром записано

double (*f)(double x)

Что это означает?

Первое слово double — это тип результата подынтегральной функции.

(*f) — формальное обозначение имени передаваемой в подпрограмму функции (это f). Перед ним записан символ * (звёздочка), означающий, что передаётся адрес функции. Скобки обязательны, иначе символ * (звёздочка) будет относится к первому слову, т.е. double.

(double x) — список формальных параметров функции, которая передаётся в функцию Integral(). У нас имеется один формальный параметр типа double, передаваемый по значению.

Как видим из примера, совсем несложно настроить функцию вычисления интеграла на работу с нужной подынтегральной функцией. Такой приём (передача имени функции в подпрограмму в качестве параметра) довольно часто применяют для реализации различных численных методов, например: нахождение корней уравнения, поиск точек экстремума, вычисление производных, определённых интегралов и т.д., что позволяет повысить универсальность программ.